RESEARCH ARTICLE
Model-based Characterization of the Parameters of Dissimilatory Sulfate Reduction Under the Effect of Different Initial Density of Desulfovibrio piger Vib-7 Bacterial Cells
Ivan Kushkevych1, 3, *, Marco Bolis2, Milan Bartos3
Article Information
Identifiers and Pagination:
Year: 2015Volume: 9
First Page: 55
Last Page: 69
Publisher ID: TOMICROJ-9-55
DOI: 10.2174/1874285801509010055
Article History:
Received Date: 20/1/2015Revision Received Date: 2/3/2015
Acceptance Date: 27/03/2015
Electronic publication date: 31/7/2015
Collection year: 2015

open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
The objective of this study was to design a model of dissimilatory sulfate reduction process using the Verhulst function, with a particular focus on the kinetics of bacterial growth, sulfate and lactate consumption, and accumulation of hydrogen sulfide and acetate. The effect of the initial density (0.12±0.011, 0.25±0.024, 0.5±0.048 and 1.0±0.096 mg cells/ml of medium) of the sulfate-reducing bacteria Desulfovibrio piger Vib-7 on the growth and dissimilatory sulfate reduction was studied. The exponential growth phase of the D. piger Vib-7 was observed for 72 hours of cultivation at the (0.12 and 0.25 mg/ml) initial concentration of bacterial cells. Sulfate and lactate were consumed incompletely during this time. The increase in the initial concentration of cells to 0.5 and 1 mg/ml led to a shortening of the exponential bacterial growth phase and a shift to the stationary phase of the growth. In the case of 0.5 mg/ml seeding, the stationary growth phase was observed in the 36th hour of cultivation. The increase in the initial concentration of cells to 1 mg/ml led to the beginning of the stationary growth phase in 24th hours of cultivation. Under these conditions, sulfate and lactate were consumed completely in the 48th hour of cultivation. The kinetic analysis of the curves of bacterial growth and the process of dissimilatory sulfate reduction by D. piger Vib-7 was carried out.
INTRODUCTION
Sulfate-reducing bacteria are prokaryotic microorganisms constituting a part intestinal microbial community in the humans and animals [1-3]. They assimilate sulfate as a terminal electron acceptor and organic compounds as the electron donor, accumulating sulfide and acetate in the process of dissimilatory sulfate reduction [4, 5]. These bacteria can also consume some organic substances (e.g. pyruvate, acetate, ethanol, succinate, butyrate, etc.) as the electron donor and carbon source [6, 7].
There are some indications that sulfate-reducing bacteria together with other infections can cause a variety of diseases (cholecystitis, abscesses of the brain and abdomen, ulcerative enterocolitis, etc.) [8-10]. The cause of ulcerative colitis is unknown but it is likely to depend on an interaction between genetic factors, which may determine the immune response or the expression of enzymes that control intracellular metabolism, and environmental factors, such as diet and the nature of the bacterial flora [11]. The Desulfovibrio genus has often been isolated from healthy and sick humans and animals [1, 2]. Perhaps, this bacterial genus can play some role in the pathogenesis of bowel diseases than other genera of sulfate-reducing bacteria.
In 1976 Moore W.E. found sulfate-reducing bacteria for the first time in human feces and identified them as Desulfomonas pigra [12]. They were later reclassified to Desulfovibrio piger [13]. Loubinoux J. et al have also established that 12 out of 100 samples of purulent peritoneal and pleural cavities in humans contained Desulfovibrio piger, D. fairfieldensis or D. desulfuricans [8, 9]. Bacteria Desulfovibrio fairfieldensis has been isolated in mono- as well as polymicrobial infections of the gastrointestinal tract. Bacteria D. desulfuricans have also been isolated from the colon during bleeding microvilli, causing bacteremia [9]. These studies confirm that the main way of the sulfate-reducing bacteria penetration in the blood is through the damaged intestinal microvilli, where bacteria can subsequently cause various infections.
To clarify the role of sulfate-reducing bacteria in the development of various human diseases, it is necessary to study the bacterial growth and process of dissimilatory sulfate reduction by the strains obtained from the intestines of healthy individuals as well as from people with various intestinal diseases, and to compare their physiological, biochemical, genetic and morphological properties.
The growth rate of the studied bacteria in the human gut can depend on many factors (including the presence of free sulfate and organic compounds). In previous studies, authors have shown that the Desulfovibrio piger Vib-7 bacterial growth depended on the concentration of sulfate and lactate as well as accumulation of sulfide and acetate in the medium [14]. Perhaps, the accumulation of sulfide and acetate can largely depend on conditions of bacterial growth, in particular on physiological and biochemical state of their cells, the total number of bacteria in the gut and on the fact, in which growth phases particular bacterial population are. The growth phases of various microbial populations have been studied and described [15-21].
Different kinetic parameters (specific and absolute rates of D. piger Vib-7 growth, sulfate and lactate consumption, sulfide and acetate accumulation, the average generation time, etc.) can be used to characterize the physiological and biochemical activities of the intestinal sulfate-reducing bacteria in the gut. Currently, methods of mathematical modeling have often been applied in microbiology [15-21]. These methods allow establishing processes of bacterial growth and dissimilatory sulfate reduction as well as determining the influence of various factors on these physiological and biochemical processes. Such approach is of particular interest in studying the dynamics of growth and process of sulfate reduction by the sulfate-reducing bacteria. The influence of different density bacterial cells in the medium on the dissimilatory sulfate reduction by the Desulfovibrio genus has been insufficiently studied. The data on the kinetic parameters of dissimilatory sulfate reduction process in the sulfate-reducing bacteria Desulfovibriopigerhas never been well-characterized and has not been studied yet.
The aim of this work was to study the process of dissimilatory sulfate reduction under the effect of different density of Desulfovibrio piger Vib-7 bacterial cells in the medium during 72 hours of cultivation, and to design a model of this process using the Verhulst function, with a particular focus on the kinetics of bacterial growth, sulfate and lactate consumption, and accumulation of sulfide and acetate.
MATERIAL AND METHODS
The object of the study was the sulfate-reducing bacteria of the Desulfovibrio piger strain Vib-7 isolated from the human large intestine and identified by the sequence analysis of the 16S rRNA gene [14, 22]. The strain has been kept in the collection of microorganisms at the Laboratory of Biotechnology, Faculty of Pharmacy, University of Veterinary and Pharmaceutical Sciences Brno (Czech Republic).
Bacteria were grown in a nutrition-modified Kravtsov-Sorokin's liquid medium [14]. Before bacteria seeding in the medium, 0.05 ml/l of sterile solution of Na2S×9H2O (1%) to initiate bacterial growth was added. A sterile 10N solution of NaOH (0.9 ml/l) in the medium (for the final pH 7.2) was used. The medium was heated in boiling water for 30 min in order to obtain an oxygen-free medium, and then cooled to 30°C. The bacteria were grown for 72 hours at 37°C under anaerobic conditions. The tubes (volume 1.5 ml) were brim-filled with medium containing bacteria and closed to provide anaerobic conditions.
To study the growth of D. piger Vib-7 and the process of dissimilatory sulfate reduction depending on the density of seeding, the bacterial strain in the Kravtsov-Sorokin's liquid medium was added to provide the initial cell seeding concentration (0.12±0.011, 0.25±0.024, 0.5±0.048 and 1.0±0.096 mg cells/ml of medium) in the medium.
Optical density of sulfate-reducing bacteria D. piger Vib-7 in the liquid medium (without Mohr's salt) was determined by the dilute suspension of the bacterial cells using the photometric method [23]. The biomass of the cells was calculated by the formula:
where C – bacterial biomass (mg cells/ml of medium); E – extinction at λ nm (λ=340 nm); n – dilution factor, times; К – coefficient of conversion, obtained gravimetrically (К=0.19).
The sulfate ion concentration in the medium was determined by the turbidimetric method after it had been precipitated by barium chloride. To stabilize the suspension, glycerol was used [24].
Sulfide concentration in the culture medium was determined by the spectrophotometric method as was described in paper [25].
Measurements of lactate concentration were carried out through the dFehydrogenation reaction using Lactate Assay Kit (Sigma-Aldrich, Catalog Number MAK064)
Accumulation of acetate ions in process of bacterial growth in the medium was determined using Acetate Assay Kit (Colorimetric, Catalog Number KA3764).
To approximate the empirical curves of dissimilatory sulfate reduction parameters, Verhulst function was used [15]:
(Equation 1)
where x – value of bacterial growth, sulfate or lactate consumption, sulfide or acetate accumulation by the D. piger Vib-7; t – time of the studied strain cultivation (hours), and A – the upper asymptote of the function (maximum of the specific parameter); C – the lower limit at which to begin the function; α and β – kinetic parameters determining the slope inflection point and form a logistic curve. Indices α and β were calculated from the linear anamorphosis obtained by taking the logarithm Verhulst function [15]:
(Equation 2)
Kinetic and statistical calculations of the RESULTS were carried out using Microsoft Excel and Origin computer programs. The research RESULTS were treated by the methods of variation statistics using Student t-test. The equation of the straight line that the best approximates the experimental data was calculated by the method of least squares. The absolute value of the correlation coefficient r was from 0.90 to 0.99. The statistical significance of the calculated parameters of line was tested by the Fisher’s F-test. The difference was reliable when P>0.95 [26]. The main result of a correlation is called Pearson’s correlation coefficient (or „r”). It is best represents the contemporary use of the simple correlation that assesses the linear relationship between two variables. The coefficient indicates the strength of the relationship, with values ranging from 0 to 1 in absolute value. The larger the magnitude of the coefficient, the stronger the relationship between the variables. The sign of the coefficient indicates the direction of the relationship as null, positive, or negative. A null relationship between variables X and Y suggests that an increase in variable X is ccompanied with both an increase and a decrease in variable Y and vice versa [27].
RESULTS AND DISCUSSION
RESULTS of our research showed that the studied sulfate-reducing bacteria, Desulfovibrio piger Vib-7, actively assimilated sulfate and lactate producing sulfide and acetate. The rates of bacterial growth and process of dissimilatory sulfate reduction depending on the number of seeding cells were significantly different from each other (Fig. 1). The exponential growth phase of the bacteria D. piger Vib-7 was observed until 72 hours of cultivation at the initial (0.12±0.011 and 0.25±0.024 mg/ml) concentration of the bacterial cells. Sulfate and lactate ions were consumed incompletely during this time. Obviously, the time of 72 hours is not sufficient for the strain D. piger Vib-7 to completely consume the acceptor and electron donor at the applied initial concentration of cells. The increase in the initial concentration of cells to 0.5±0.048 and 1.0±0.096 mg/ml led to a shortening of the exponential bacterial growth phase and an earlier shift to the stationary phase of growth. In the case of seeding of 0.5±0.048 mg/ml, the stationary phase of growth was observed since the 36th hour of cultivation. An increase in the initial concentration of cells up to 1.0±0.096 mg/ml led to the onset of the stationary phase after 24th hours of cultivation. Under these conditions, sulfate and lactate were consumed completely by the 48th hour of cultivation.
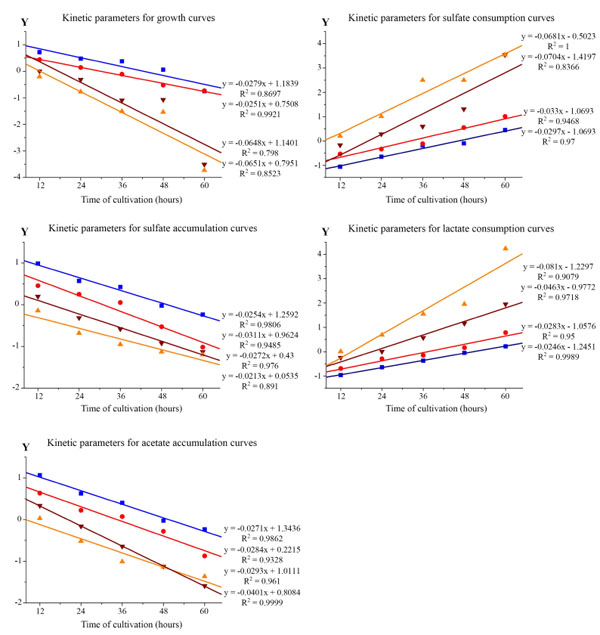
The next task of our study was to carry out a kinetic analysis of the curve of growth and to study the process of sulfate reduction depending on time of cultivation at various initial D. piger Vib-7 cell densities. The RESULTS of these studies showed that curves of the D. piger Vib-7 growth, sulfide and acetate accumulation had a characteristic s-shaped (sigmoidal shape) (Fig. 1). Verhulst logistic function is the most convenient of the dynamic models used to describe the sigmoid curves [15-21, 28]. From equation 2, the relationship between the variables and t was described by linear regressions (Fig. 2).
The determination coefficient R2 is the criterion for assessing the communication linearity [26]. The error of regression deviation (Sxt) and delimits of the argument t = t1, and a minimum (in point T2) at a value of the confidence interval for the 5% significance level for a theoretical regression line was calculated. The adequacy of the approximation model by using Fisher's exact test was evaluated [18].
A characteristic feature of the sigmoid curve type is the presence of an inflection point, reflecting the moment of transition of the increasing growth rate to decreasing. To determine it, it is necessary to calculate the first and second derivatives of the function (1). The first derivative of Verhulst, representing an absolute rate of specific parameter by the D. piger Vib-7 was found by equation:
(Equation 3) [15].
The graph of the function has one extreme (maximum) corresponding to the maximum value of the absolute rate of bacterial growth when the argument t = te,where (if t ≥ 0 values α > 0 and β < 0).
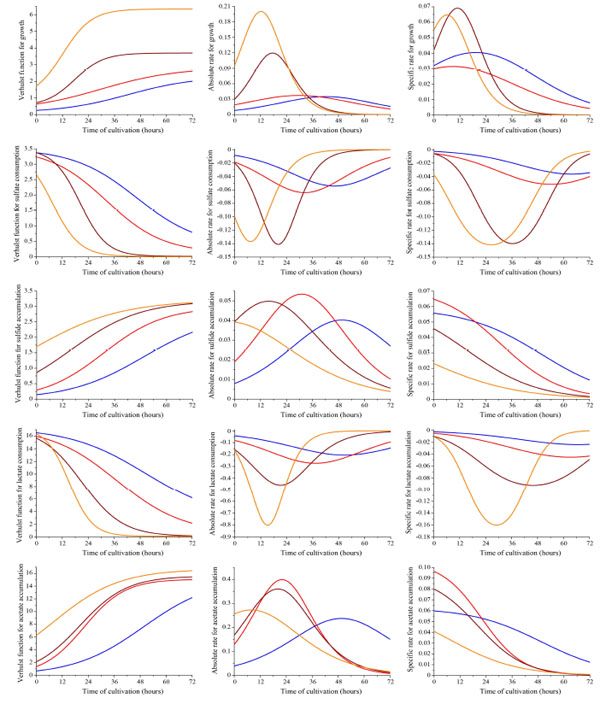
The parameter characterizing the dynamics of the bacterial growth, sulfate and lactate consumption, sulfide and acetate accumulation by the D. piger Vib-7 correspond to the absolute rate and the relative (specific) rate . This value reflects the increase in biomass (or sulfate and lactate consumption, sulfide and acetate accumulation by D. piger Vib-7) dx per unit of time dt and per unit of specific parameter х (h-1) (Fig. 3).
Based on experimental data, values of kinetic parameters of the dissimilatory sulfate reduction depending on the initial D. piger Vib-7 cell concentration were calculated (Table 1).
Mean zones of microbial growth inhibition (in mm), which were caused by the six most effective venom concentrations of six snakes.
| Parameters | Initial biomass (mg/ml) | А | С | α | β |
|---|---|---|---|---|---|
| Bacterial growth | 0.12±0.011 | 2.291±0.208 | 0.119±0.011 | 1.183939±0.107631 | -0.02793±0.00254 |
| 0.25±0.024 | 2.821±0.256 | 0.249±0.023 | 0.750815±0.068256 | -0.02515±-0.00229 | |
| 0.5±0.048 | 3.701±0.336 | 0.499±0.045 | 1.140081±0.103644 | -0.06484±0.00589 | |
| 1.0±0.096 | 6.341±0.576 | 0.999±0.091 | 0.795138±0.072285 | -0.06512±0.00592 | |
| Sulfate consumption | 0.12±0.011 | 3.501±0.315 | 0.329±0.030 | -1.37743±0.124093 | 0.029715±0.002677 |
| 0.25±0.024 | 3.501±0.318 | 0.129±0.012 | -1.06932±0.097211 | 0.032967±0.002997 | |
| 0.5±0.048 | 3.501±0.313 | 0.019±0.002 | -1.4197±0.126759 | 0.070392±0.006285 | |
| 1.0±0.096 | 3.501±0.310 | 0.009±0.001 | -0.50228±0.044450 | 0.068137±0.006030 | |
| Sulfide accumulation | 0.12±0.011 | 2.751±0.250 | 0 | 1.259196±0.114472 | -0.02537±0.002306 |
| 0.25±0.024 | 2.981±0.271 | 0 | 0.962374±0.087489 | -0.0311±0.002827 | |
| 0.5±0.048 | 3.181±0.289 | 0 | 0.430032±0.039094 | -0.02718±0.002471 | |
| 1.0±0.096 | 3.201±0.291 | 0 | -0.05352±0.004865 | 0.02132±0.001938 | |
| Lactate consumption | 0.12±0.011 | 17.301±1.559 | 2.849±0.257 | -1.24506±0.112168 | 0.024571±0.002214 |
| 0.25±0.024 | 17.301±1.573 | 0.579±0.053 | -1.05761±0.096146 | 0.028336±0.002576 | |
| 0.5±0.048 | 17.301±1.545 | 0.089±0.008 | -0.97715±0.087246 | 0.046259±0.004130 | |
| 1.0±0.096 | 17.301±1.531 | 0.099±0.009 | -1.22972±0.108825 | 0.080994±0.007168 | |
| Acetate accumulation | 0.12±0.011 | 15.201±1.382 | 0 | 1.343622±0.122147 | -0.02712±0.002465 |
| 0.25±0.024 | 15.103±1.373 | 0 | 1.011105±0.091919 | -0.04589±0.004172 | |
| 0.5±0.048 | 15.591±1.417 | 0 | 0.808435±0.073494 | -0.04012±0.003647 | |
| 1.0±0.096 | 16.681±1.516 | 0 | 0.22151±0.020137 | -0.02839±0.002581 |
Comments: Statistical significance of the values are means M±m, n = 5.
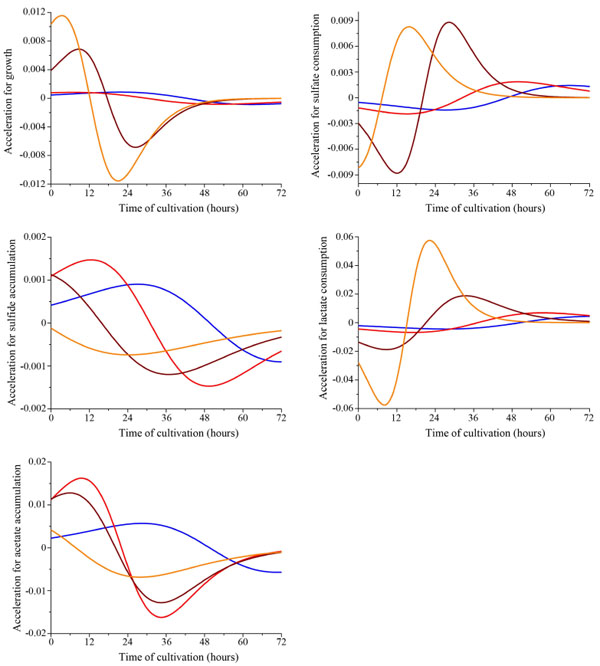
The second derivative of the function (1) that characterizes the acceleration of bacterial growth, sulfate and lactate consumption, sulfide and acetate accumulation by the D. piger Vib-7 were determined by the following equation:
(Equation 4)
The graph of the function (Fig. 4) has two extremes – maximum (in point Т1) where the argument t = t2, and at t = te function is equal to zero which is a sufficient condition for the existence of an inflection point on the graph functions.
To determine the argument values t1and t2 that correspond to two points of inflection on the graph of the first derivative function the third derivative of Verhulst function was calculated (under the condition ), and the following equations were derived:
(Equation 5)
Dynamics of bacterial population growth have isolated several stages corresponding to certain physiological activities of cells. The calculation of coordinates of critical points of Т1 (х1; t1), Т2(х2; t2)and the inflection point of Тe (хe; te) for the logistic curve allows a clear distinction between the time the main phasesof D. piger Vib-7 growth and process of dissimilatory sulfate reduction. The onset of the D. piger Vib-7 growth comprising of the lag phase and accelerate growth phase was observed at the time of INTRODUCTION of bacterial strain into the Kravtsov-Sorokin's liquid medium (at t = 0) and continued until time t = t1 where the acceleration of bacterial growth reached its maximum value. Almost linear growth of D. piger Vib-7 cells (exponential phase) lasted for a period of time interval from t = t1to the point of inflection of the curve at t = te; followed by the phase of slower growth (the time from the point t = te to time moment t = t2), which corresponded to the maximum value of the negative acceleration (deceleration) of the D. piger Vib-7 growth. Similar RESULTS were obtained by Moisa L.N. et al. Authors used kinetics analysis method for growth curves based on the Verhulst logistic function to determine some growth parameters describing physiological activity of the E. coli strain expressing a recombinant β-galactosidase protein controlled by С1857 gene. Moisa L.N. et al. also calculated and described several growth points critical for the development of E. coli microbial population, such as the transition of increasing growth speed to the decreasing one (the inflection point of the curve – Te), the maximal growth acceleration phase (the point T1), and the negative growth acceleration (slowing) phase (the point T2) [15]. It is well known that the growth phase and the initial cell concentrations might have a significant influence on the duration of the cultivation cycle [15-21, 28].
The obtained data (presented in the Table 2) showed the growth rate of the D. piger Vib-7, sulfate and lactate consumption, accumulation of sulfide and acetate as well as the duration of the exponential growth phase. These processes depend on the initial cell density in the Kravtsov-Sorokin's medium. The increase in the initial D. piger Vib-7 cell density to 1 mg/ml in the medium led to a reduction in the duration of the exponential phase of bacterial growth. The duration of the exponential phase of growth (te) was 12 hours at 1.0±0.096 mg/ml; while this period was significantly longer (42 hours) at 0.12±0.011 mg/ml initial D. piger Vib-7 cell density.
Kinetic parameters of the dissimilatory sulfate reduction by Desulfovibrio piger Vib-7 calculated from the approximation model of the logistic Verhulst functions.
| Parameters | Initial biomass (mg/ml) | x0 | µ0 | t1 | t2 | te | µmax | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bacterial growth |
0.12±0.011 | 0.2525±0.0230 | 0.0319±0.0029 | 21.9103±1.9918 | 62.8635±5.7149 | 42.3869±3.8534 | 0.0404±0.0037 | ||||||||
| 0.25±0.024 | 0.6367±0.0579 | 0.0299±0.0027 | 7.1125±0.6466 | 52.5988±4.7817 | 29.8557±2.7142 | 0.0313±0.0028 | |||||||||
| 0.5±0.048 | 0.7152±0.0650 | 0.0421±0.0038 | 8.7622±0.7966 | 26.4043±2.4004 | 17.5833±1.5985 | 0.0691±0.0063 | |||||||||
| 1.0±0.096 | 1.7369±0.1579 | 0.0549±0.0050 | 3.4272±0.3116 | 20.9925±1.9084 | 12.2099±1.1100 | 0.0647±0.0059 | |||||||||
| Sulfate consumption | 0.12±0.011 | 3.3733±0.3039 | -0.0025±0.0002 | 65.6035±5.9102 | 27.1074±2.4421 | 46.3554±4.1762 | -0.0025±0.0002 | ||||||||
| 0.25±0.024 | 3.2361±0.2942 | -0.0057±0.0005 | 49.7854±4.5259 | 15.0871±1.3716 | 32.4362±2.9487 | -0.0057±0.0005 | |||||||||
| 0.5±0.048 | 3.3734±0.3012 | -0.0059±0.0005 | 28.2936±2.5262 | 12.0432±1.0753 | 20.1684±1.8008 | -0.0059±0.0005 | |||||||||
| 1.0±0.096 | 2.6653±0.2359 | -0.0374±0.0033 | 15.7656±1.3952 | -1.0225±0.0905 | 7.3715±0.6523 | -0.0024±0.0002 | |||||||||
| Sulfide accumulation | 0.12±0.011 | 0.1426±0.0130 | 0.0558±0.0051 | 27.0865±2.4624 | 72.1707±6.5610 | 49.6286±4.5117 | 0.0558±0.0051 | ||||||||
| 0.25±0.024 | 0.2922±0.0266 | 0.0648±0.0059 | 12.5556±1.1414 | 49.3419±4.4856 | 30.9488±2.8135 | 0.0648±0.0059 | |||||||||
| 0.5±0.048 | 0.8609±0.0783 | 0.0457±0.0042 | -5.2212±0.4747 | 36.8641±3.3513 | 15.8214±1.4383 | 0.0457±0.0042 | |||||||||
| 1.0±0.096 | 1.6985±0.1544 | 0.0231±0.0021 | -29.3369±2.6670 | 24.3161±2.2106 | 2.5104±0.2282 | 0.0230±0.0021 | |||||||||
| Lactate consumption | 0.12±0.011 | 16.5232±1.4886 | -0.0025±0.0002 | 73.9492±6.6621 | 27.3945±2.4680 | 50.6718±4.5650 | -0.0025±0.0002 | ||||||||
| 0.25±0.024 | 15.9544±1.4504 | -0.0051±0.0005 | 57.5076±5.2280 | 17.1392±1.5581 | 37.3234±3.3930 | -0.0051±0.0005 | |||||||||
| 0.5±0.048 | 15.6598±1.3982 | -0.0101±0.0009 | 33.4879±2.9900 | 8.75958±0.7821 | 21.1237±1.8860 | -0.0101±0.0009 | |||||||||
| 1.0±0.096 | 16.3438±1.4464 | -0.0103±0.0009 | 22.2445±1.9685 | 8.1212±0.7187 | 15.1829±1.3436 | -0.0008±0.0001 | |||||||||
| Acetate accumulation | 0.12±0.011 | 0.6582±0.0598 | 0.0598±0.0054 | 28.4587±2.5872 | 70.6445±6.4222 | 49.5516±4.5047 | 0.0598±0.0054 | ||||||||
| 0.25±0.024 | 1.3403±0.1218 | 0.0964±0.0088 | 9.5692±0.8699 | 34.4944±3.1359 | 22.0318±2.0029 | 0.0964±0.0088 | |||||||||
| 0.5±0.048 | 2.0966±0.1906 | 0.0799±0.0073 | 5.8945±0.5359 | 34.4062±3.1278 | 20.1503±1.8318 | 0.0799±0.0073 | |||||||||
| 1.0±0.096 | 6.2578±0.5689 | 0.0408±0.0037 | -12.3425±1.1220 | 27.9458±2.5405 | 7.8016±0.7092 | 0.0408±0.0037 | |||||||||
| Parameters | Initial biomass (mg/ml) | T1 (maximum acceleration of growth) | Te (the point of curve inflection of growth acceleration) | T2 (negative acceleration - deceleration of growth) | |||||||||||
| dx/dt1 | µ1 | dx/dte | µe | dx/dt2 | µ2 | ||||||||||
| Bacterial growth |
0.12±0.011 | 0.0233±0.0021 | 0.0403±0.0037 | 0.0349±0.0032 | 0.0289±0.0026 | 0.0233±0.0021 | 0.0128±0.0012 | ||||||||
| 0.25±0.024 | 0.0248±0.0023 | 0.0313±0.0028 | 0.0372±0.0034 | 0.0242±0.0022 | 0.0248±0.0023 | 0.0109±0.0010 | |||||||||
| 0.5±0.048 | 0.0797±0.0072 | 0.0678±0.0062 | 0.1195±0.0109 | 0.0569±0.0052 | 0.0797±0.0072 | 0.0263±0.0024 | |||||||||
| 1.0±0.096 | 0.1335±0.0121 | 0.0545±0.0050 | 0.2003±0.0182 | 0.0546±0.0050 | 0.1121±0.0102 | 0.0256±0.0023 | |||||||||
| Sulfate consumption | 0.12±0.011 | -0.0362±0.0033 | -0.0362±0.0033 | -0.0543±0.0049 | -0.0283±0.0025 | -0.0362±0.0033 | -0.0128±0.0012 | ||||||||
| 0.25±0.024 | -0.0427±0.0039 | -0.0507±0.0046 | -0.0639±0.0058 | -0.0353±0.0032 | -0.0427±0.0039 | -0.0153±0.0014 | |||||||||
| 0.5±0.048 | -0.0941±0.0084 | -0.1246±0.0111 | -0.1411±0.0126 | -0.0802±0.0072 | -0.0941±0.0084 | -0.0340±0.0030 | |||||||||
| 1.0±0.096 | -0.0913±0.0081 | -0.1222±0.0108 | -0.1369±0.0121 | -0.0780±0.0069 | -0.0913±0.0081 | -0.0330±0.0029 | |||||||||
Comments: t1, tе ,t2 are critical points on curves of the dissimilatory sulfate reduction by the strain Desulfovibrio piger Vib-7; х is the bacterial growth, sulfate and lactate consumption, sulfide and acetate accumulation; x0 is initial conditions of the strain at time t = 0; t is the time of the bacterial cultivation; te is the duration of the exponential phase; dx/dt is the absolute rate; µ0 is the specific rate at time t = 0; µmax is the maximum specific rate. Statistical significance of the values are means M±m, n = 5.
A similar pattern was observed in the process of the dissimilatory sulfate reduction. In this case, the duration of maximal intensity of sulfate and lactate consumption as well as accumulation of sulfide and acetate were observed for a significantly longer period of time (te) at the lowest initial D. piger Vib-7 cell density (0.12±0.011 mg/ml) after 46, 49, 50 and, 49 hours, respectively. Under the condition of the highest initial bacterial cell density (1 mg/ml), the maximal intensity (te) in time of the sulfate reduction process was significantly shorter.
A pronounced tendency of the kinetics of absolute and specific rates of the growth, sulfate and lactate consumption, and accumulation of sulfide and acetate were determined. Graphs imply that the value of the absolute growth rate reached its maximum value at the point of the logistic curve inflection (see Fig. 3). The highest value of absolute rates of the D. piger Vib-7 growth was (0.2003±0.0182 ) at 1.0±0.096 mg/ml initial bacterial cell density in the medium; while the maximal intensity (te) was achieved after approximately 12 hours.
The lowest value of absolute rates (0.0349±0.0032) was observed at 0.12±0.011 mg/ml initial bacterial cell density (te was calculated after 42 hours of growth). The maximal absolute rates of sulfate consumption (-0.1411±0.0126 mM/hour) and accumulation of sulfide (0.0534±0.0049 mM/hour) were determined respectively at 0.5±0.048 and 0.12±0.011 mg/ml initial bacterial cell density in the medium. The absolute rate of lactate consumption increased from -0.2044±0.0184 to -0.8020±0.0710 mM/hour with the increase in the initial D. piger Vib-7 cell density from 0.12±0.011 to 1.0±0.096 mg/ml in the medium, respectively. However, the highest absolute rate of the acetate accumulation (0.3989±0.0363 mM/hour) was determined at 0.25±0.024 mg/ml initial bacterial cell density. The highest value of the specific D. piger Vib-7 growth rate and sulfate reduction parameters (µmax) was observed in the area of exponential growth (in particular in the range of critical points of growth from Т1 to Те).
Thus, the increase in the initial bacterial cell dose (х0) led to the increase in the absolute rate of the D. piger Vib-7 growth and initiated the process of the dissimilatory sulfate reduction. However, the reduction of the duration of these processes (te) was observed. The determination of the kinetics in the exponential D. piger Vib-7 growth phase and the dissimilatory sulfate reduction process are of particular interest to characterize the physiological and biochemical state of the sulfate-reducing bacteria in the human intestine.
A correlation analysis is related in the sense that both deal with relationships among variables. The correlation coefficient is a measure of linear association between two variables [27]. Therefore, the next task of the study was to perform the correlation analysis between parameters of dissimilatory sulfate reduction depending on initial density of Desulfovibriopiger Vib-7 bacterial cells.
The correlation coefficients (r) between these parameters were defined (Table 3). A strong inversely negative correlation between biomass and sulfate, biomass and lactate, sulfate and sulfide, sulfate and acetate, lactate and acetate, lactate and sulfide was demonstrated. A strong positive correlation between biomass and sulfide, biomass and acetate, lactate and sulfate, acetate and sulfide was showed. The correlation coefficient ranges from -1.0 to +1.0. The closer r is to +1 or -1, the more closely the two variables are related. If r is close to 0, it means there is no relationship between the variables. If r is positive, it means that as one variable gets larger the other gets larger. If r is negative it means that as one gets larger, the other gets smaller (often called an “inverse” correlation). While correlation coefficients are normally reported as r = (a value between -1 and +1), squaring them makes then easier to understand. Values between 0.7 and 1.0 (-0.7 and -1.0) indicate a strong positive (negative) linear relationship via a firm linear rule [27].
Correlation coefficients (r) between parameters of dissimilatory sulfate reduction depending on initial density of Desulfovibrio piger Vib-7 bacterial cells.
| Parameters | Biomass | Sulfate | Sulfide | Lactate | Acetate |
|---|---|---|---|---|---|
| 0.12±0.011 mg/ml | |||||
| Biomass | 1 | -0.9822±0.0893 | 0.9737±0.0875 | -0.9743±0.0882 | 0.972±0.0884 |
| Sulfate | -0.9822±0.0893 | 1 | -0.9812±0.0892 | 0.9878±0.0888 | -0.9835±0.0874 |
| Sulfide | 0.9737±0.0875 | -0.9812±0.0892 | 1 | -0.9981±0.0905 | 0.9996±0.0909 |
| Lactate | -0.9743±0.0882 | 0.9878±0.0888 | -0.9981±0.0905 | 1 | -0.9985±0.0908 |
| Acetate | 0.972±0.0884 | -0.9835±0.0874 | 0.9996±0.0909 | -0.9985±0.0908 | 1 |
| 0.25±0.024 mg/ml | |||||
| Biomass | 1 | -0.9859±0.0896 | 0.9912±0.0901 | -0.9773±0.0888 | 0.9875±0.0898 |
| Sulfate | -0.9859±0.0896 | 1 | -0.9988±0.0908 | 0.9831±0.0894 | -0.9890±0.0899 |
| Sulfide | 0.9912±0.0901 | -0.9988±0.0908 | 1 | -0.9854±0.0896 | 0.9920±0.0902 |
| Lactate | -0.9773±0.0888 | 0.9831±0.0894 | -0.9854±0.0896 | 1 | -0.9979±0.0907 |
| Acetate | 0.9875±0.0898 | -0.9890±0.0899 | 0.9920±0.0902 | -0.9979±0.0907 | 1 |
| 0.5±0.048 mg/ml | |||||
| Biomass | 1 | -0.9878±0.0898 | 0.9873±0.0821 | -0.9771±0.0835 | 0.9821±0.0893 |
| Sulfate | -0.9878±0.0898 | 1 | -0.9968±0.0906 | 0.9895±0.0900 | -0.9951±0.0905 |
| Sulfide | 0.9873±0.0821 | -0.9968±0.0906 | 1 | -0.9814±0.0892 | 0.9925±0.0902 |
| Lactate | -0.9771±0.0835 | 0.9895±0.0900 | -0.9814±0.0892 | 1 | -0.9942±0.0904 |
| Acetate | 0.9821±0.0893 | -0.9951±0.0905 | 0.9925±0.0902 | -0.9942±0.0904 | 1 |
| 1.0±0.096 mg/ml | |||||
| Biomass | 1 | -0.9988±0.0908 | 0.9964±0.0906 | -0.9931±-0.0903 | 0.9898±0.0900 |
| Sulfate | -0.9988±0.0908 | 1 | -0.9961±0.0904 | 0.9930±0.0903 | -0.9883±0.0898 |
| Sulfide | 0.9964±0.0906 | -0.9961±0.0904 | 1 | -0.9922±0.0904 | 0.9930±0.0901 |
| Lactate | -0.9931±0.0903 | 0.9930±0.0903 | -0.9922±0.0904 | 1 | -0.9980±0.0907 |
| Acetate | 0.9898±0.0900 | -0.9883±0.0898 | 0.9930±0.0901 | -0.9980±0.0907 | 1 |
Comments: Statistical significance of the values are means M±m, n = 5.
The systematic statistical analysis of the parameters of dissimilatory sulfate reduction was also performed. The RESULTS of the studies showed that the variance, pooled variance, t-statistics, P (T⇐t) one-way, P (T⇐t) two-way were quite various at the combinations of different parameters (in particular biomass and sulfate, biomass and lactate, sulfate and sulfide, sulfate and acetate, lactate and acetate, lactate and sulfide etc.). These statistical parameters also depended on initial density of D.piger Vib-7 bacterial cells (Table 4). However, t critical one-way (1.7823±0.1620) and t critical two-way (2.1788±0.1981) were similar for each of the parameters.
The systematic statistical analysis of the parameters of dissimilatory sulfate reduction depending on initial density of Desulfovibrio piger Vib-7 bacterial cells.
| Parameters | 0.12±0.011 mg/ml | |||||
|---|---|---|---|---|---|---|
| Average | Variance | Pooled Variance | t-statistics | P (T<=t) one-way | P (T<=t) two-way | |
| Biomass and Sulfate | 1.0554±0.0959 | 0.6355±0.0578 | 0.9755±0.0887 | -2.1939±0.1994 | 0.0243±0.002209 | 0.0487±0.004427 |
| 2.2136±0.2012 | 1.3154±0.1196 | |||||
| Biomass and Lactate | 1.0554±0.0959 | 0.6355±0.0578 | 12.8362±1.1669 | -5.5955±0.5087 | 0.00005±0.000001 | 0.0001±0.000009 |
| 11.7711±1.0701 | 25.0369±2.2761 | |||||
| Sulfate and Sulfide | 2.2136±0.2012 | 1.3154±0.1196 | 1.1192±0.1017 | 2.0235±0.1840 | 0.0329±0.002991 | 0.0659±0.005991 |
| 1.0693±0.0972 | 0.9231±0.0839 | |||||
| Sulfate and Acetate | 2.2136±0.2012 | 1.3154±0.1196 | 15.0147±1.3650 | -1.7612±0.1601 | 0.0518±0.004709 | 0.1036±0.009418 |
| 5.8614±0.5329 | 28.7140±2.6104 | |||||
| Lactate and Acetate | 11.7711±1.0701 | 25.0369±2.2761 | 26.8754±2.4432 | 2.1326±0.1939 | 0.0271±0.002464 | 0.0543±0.004936 |
| 5.8614±0.5329 | 28.7140±2.6104 | |||||
| Lactate and Sulfide | 11.7711±1.0701 | 25.0369±2.2761 | 12.9800±1.1800 | -5.5572±0.5052 | 0.00005±0.000001 | 0.0001±0.000009 |
| 1.0693±0.0972 | 0.9231±0.0839 | |||||
| Biomass and Sulfide | 1.0554±0.0959 | 0.6355±0.0578 | 0.7793±0.0708 | -0.0295±0.0027 | 0.4885±0.044409 | 0.9769±0.088809 |
| 1.0693±0.0972 | 0.9231±0.0839 | |||||
| Biomass and Acetate | 1.0554±0.0959 | 0.6355±0.0578 | 14.6748±1.3341 | -2.3471±0.2134 | 0.0185±0.001682 | 0.0369±0.003355 |
| 5.8614±0.5329 | 28.7140±2.6104 | |||||
| Lactate and Sulfate | 11.7711±1.0701 | 25.0369±2.2761 | 13.1761±1.1978 | -4.9259±- 0.4478 |
0.0002±0.000018 | 0.0004±0.000036 |
| 2.2136±0.2012 | 1.3154±0.1196 | |||||
| Acetate and Sulfide | 5.8614±0.5329 | 28.7140±2.6104 | 14.8186±1.3471 | -2.3290±0.2117 | 0.0191±0.001736 | 0.0381±0.003464 |
| 1.0693±0.0972 | 0.9231±0.0839 | |||||
| Biomass and Sulfate | 1.6657±0.1514 | 0.8127±0.0739 | 1.2149±0.1104 | -0.1115±0.0101 | 0.4565±0.041500 | 0.9130±0.083000 |
| 1.7314±0.1574 | 1.6171±0.1470 | |||||
| Biomass and Lactate | 1.6657±0.1514 | 0.8127±0.0739 | 18.5288±1.6844 | -3.2947±0.2995 | 0.0032±0.000291 | 0.0064±0.000582 |
| 9.2464±0.8406 | 36.2449±3.2950 | |||||
| Sulfate and Sulfide | 1.7314±0.1574 | 1.6171±0.1470 | 1.4101±0.1282 | 0.1981±0.0180 | 0.4232±0.038473 | 0.8463±0.076936 |
| 1.6057±0.1460 | 1.2031±0.1094 | |||||
| Sulfate and Acetate | 1.7314±0.1574 | 1.6171±0.1470 | 15.7132±1.4285 | -2.8038±0.2549 | 0.0080±0.000727 | 0.0159±0.001445 |
| 7.6721±0.6975 | 29.8092±2.7099 | |||||
| Lactate and Acetate | 9.2464±0.8406 | 36.2449±3.2950 | 33.0271±3.0025 | 0.5125±0.0466 | 0.3088±0.028073 | 0.6176±0.056145 |
| 7.6721±0.6975 | 29.8092±2.7099 | |||||
| Lactate and Sulfide | 9.2464±0.8406 | 36.2449±3.2950 | 18.7240±1.7022 | -3.3035±0.3003 | 0.0032±0.000291 | 0.0063±0.000573 |
| 1.6057±0.1460 | 1.2031±0.1094 | |||||
| Biomass and Sulfide | 1.6657±0.1514 | 0.8127±0.0739 | 1.0079±0.0916 | 0.1118±0.0102 | 0.4564±0.041491 | 0.9128±0.082982 |
| 1.6057±0.1460 | 1.2031±0.1094 | |||||
| Biomass and Acetate | 1.6657±0.1514 | 0.8127±0.0739 | 15.3110±1.3919 | -2.8718±0.2611 | 0.0070±0.000636 | 0.0140±0.001273 |
| 7.6721±0.6975 | 29.8092±2.7099 | |||||
| Lactate and Sulfate | 9.2464±0.8406 | 36.2449±3.2950 | 18.9310±1.7210 | -3.2313±0.2938 | 0.0036±0.000327 | 0.0072±0.000655 |
| 1.7314±01574 | 1.6171±0.1470 | |||||
| Acetate and Sulfide | 7.6721±0.6975 | 29.8092±2.7099 | 15.5061±1.4096 | -2.8821±0.2620 | 0.0069±0.000627 | 0.0138±0.001255 |
| 1.6057±0.1460 | 1.2031±0.1094 | |||||
| Biomass and Sulfate | 2.7900±0.2536 | 1.3764±0.1251 | 1.5278±0.1389 | 2.5492±0.2317 | 0.0128±0.001164 | 0.0255±0.002318 |
| 1.1057±0.1005 | 1.6793±0.1527 | |||||
| Biomass and Lactate | 2.7900±0.2536 | 1.3764±0.1251 | 22.0498±2.0045 | -1.2971±0.1179 | 0.1095±0.009955 | 0.2190±0.019909 |
| 6.0457±0.5496 | 42.7233±3.8839 | |||||
| Sulfate and Sulfide | 1.1057±0.1005 | 1.6793±0.1527 | 1.4892±0.1354 | -1.5615±0.1420 | 0.0722±0.006564 | 0.1444±0.013127 |
| 2.1243±0.1931 | 1.2991±0.1181 | |||||
| Sulfate and Acetate | 1.1057±0.1005 | 1.6793±0.1527 | 18.4672±1.6788 | -4.0039±0.3640 | 0.0009±0.000082 | 0.0017±0.000155 |
| 10.3029±0.9366 | 35.2552±3.2050 | |||||
| Lactate and Acetate | 6.0457±0.5496 | 42.7233±3.8839 | 38.9892±3.5445 | -1.2755±0.1160 | 0.1131±0.010282 | 0.2263±0.020573 |
| 10.3029±0.9366 | 35.2552±3.2050 | |||||
| Lactate and Sulfide | 6.0457±0.5496 | 42.7233±3.8839 | 22.0112±2.0010 | -1.5637±0.1422 | 0.0719±0.006536 | 0.1439±0.013082 |
| 2.1243±0.1931 | 1.2991±0.1181 | |||||
| Biomass and Sulfide | 2.7900±0.2536 | 1.3764±0.1251 | 1.3377±0.1216 | 1.0768±0.0979 | 0.1514±0.013764 | 0.3027±0.027518 |
| 2.1243±0.1931 | 1.2991±0.1181 | |||||
| Biomass and Acetate | 2.7900±0.2536 | 1.3764±0.1251 | 18.3158±1.6651 | -3.2842±0.2986 | 0.0033±0.000300 | 0.0065±0.000591 |
| 10.3029±0.9366 | 35.2552±3.2050 | |||||
| Lactate and Sulfate | 6.0457±0.5496 | 42.7233±3.8839 | 22.2013±2.0183 | -1.9614±0.1783 | 0.0367±0.003336 | 0.0734±0.006673 |
| 1.1057±0.1005 | 1.6793±0.1527 | |||||
| Acetate and Sulfide | 10.3029±0.9366 | 35.2552±3.2050 | 18.2771±1.6616 | -3.5790±0.3254 | 0.0019±0.000173 | 0.0038±0.000345 |
| 2.1243±0.1931 | 1.2991±0.1181 | |||||
| Biomass and Sulfate | 5.1100±0.4645 | 3.8045±0.3459 | 2.7589±0.2508 | 4.9124±0.4466 | 0.0002±0.000018 | 0.0004±0.000036 |
| 0.7486±0.0681 | 1.7134±0.1558 | |||||
| Biomass and Lactate | 5.1100±0.4645 | 3.8045±0.3459 | 23.1217±2.1020 | 0.3196±0.0291 | 0.3774±0.034309 | 0.7548±0.068618 |
| 4.2886±0.3899 | 42.4390±3.8581 | |||||
| Sulfate and Sulfide | 0.7486±0.0681 | 1.7134±0.1558 | 1.4972±0.1361 | -2.4769±0.2252 | 0.0146±0.001327 | 0.0291±0.002645 |
| 2.3686±0.2153 | 1.2810±0.1165 | |||||
| Sulfate and Acetate | 0.7486±0.0681 | 1.7134±0.1558 | 19.2582±1.7507 | -4.8137±0.4376 | 0.0002±0.000018 | 0.0004±0.000036 |
| 12.0400±1.0945 | 36.8029±3.3457 | |||||
| Lactate and Acetate | 4.2886±0.3899 | 42.4390±3.8581 | 39.6209±3.6019 | -2.3038±0.2094 | 0.0200±0.001714 | 0.0399±0.003627 |
| 12.0400±1.0945 | 36.8029±3.3457 | |||||
| Lactate and Sulfide | 4.2886±0.3899 | 42.4390±3.8581 | 21.8600±1.9873 | -0.7683±0.0698 | 0.2286±0.020782 | 0.4572±0.041564 |
| 2.3686±0.2153 | 1.2810±0.1165 | |||||
| Biomass and Sulfide | 5.1100±0.4645 | 3.8045±0.3459 | 2.5427±0.2312 | 3.2163±0.2924 | 0.0037±0.000336 | 0.0074±0.000673 |
| 2.3686±0.2153 | 1.2810±0.1165 | |||||
| Biomass and Acetate | 5.1100±0.4645 | 3.8045±0.3459 | 20.3037±1.8458 | -2.8773±0.2616 | 0.0070±0.000636 | 0.0139±0.001264 |
| 12.0400±1.0945 | 36.8029±3.3457 | |||||
| Lactate and Sulfate | 4.2886±0.3899 | 42.4390±3.8581 | 22.0762±2.0069 | -1.4095±0.1281 | 0.0920±0.008364 | 0.1841±0.016736 |
| 0.7486±0.0681 | 1.7134±0.1558 | |||||
| Acetate and Sulfide | 12.0400±1.0945 | 36.8029±3.3457 | 19.0420±1.7311 | -4.1464±0.3769 | 0.0007±0.000064 | 0.0014±0.000127 |
| 2.3686±0.2153 | 1.2810±0.1165 | |||||
Comments: Observation is equal to 7; hypothetical mean difference is equal to 0; df is equal to 12; t critical one-way is equal to 1.7823±0.1620; t critical two-way is equal to 2.1788±0.1981. Statistical significance of the values are means M±m, n = 5
Taking into consideration all the obtained RESULTS, it should be noted that the logistic sigmoid curves are widely used to describe various processes of bacterial growth [15-21, 28], which are supported by the RESULTS of these studies. The mathematical model of the D. piger Vib-7 intensity growth and the sulfate reduction process, which was described, can help provide a more detailed understanding of the etiological role of sulfate-reducing bacteria in the development of inflammatory human bowel processes and diseases [29].
CONCLUSION
Based on our RESULTS, we can claim that the initial bacterial cell dose and thegrowth phase of the D. piger Vib-7 affect absolute and specific rates of sulfate and lactate consumption, accumulation of sulfide and acetate, and the growth of the studied bacteria in the human colon. The universal nature of the logistic function suggests that it can be used as a method to determine the kinetics of the D. piger Vib-7 growth and assimilation of sulfate and lactate, as well as accumulation of sulfide and acetate. Strong negative and positive correlations between the parameters were demonstrated. This method might be used to assess the growth of other studied sulfate-reducing bacteria in the human intestine.
Such an approach allows for selection of the optimal conditions for the bacterial assimilation of sulfate and lactate and also the accumulation of sulfide and acetate for the purpose of preventing ulcerative colitis, inflammatory bowel disease and colon cancer.
These studies are also prospective for creation the animal models of the inflammatory bowel diseases and ulcerative colitis using the sulfate-reducing bacteria. The described mathematical model can be applied for calculation rate of the bacterial growth depending on the concentration of substrate (lactate and sulfate) in the organism. Therefore it can help to calculate the concentration of hydrogen sulfide and acetate as well as absolute and specific velocities of accumulation of these toxic compounds in the gut. It is, in turn, very important and useful for disease observation, its etiology and microbiological control of the inflammatory bowel processes and diseases development involving the sulfate-reducing bacteria.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This study was supported by University of Veterinary and Pharmaceutical Sciences Brno (project OPVK „Pharmaco-toxicological evaluation of newly synthesized (isolated) compounds as an integration tool for pre-clinical disciplines at VFU Brno” CZ.1.07/2.3.00/30.0053). The authors express their gratitude to Mark Scott from University of Mary Washington (Fredericksburg, Virginia, USA) for his assistance and critical reading of the manuscript. The authors also express their gratitude to Dr. Yurij J. Beno from Biophysics Department, Faculty of Biology, Ivan Franko National University of Lviv (Ukraine) for his assistance in perform the correlation and statistical analysis.